November 23 (11/23) is Fibonacci Day, a special day in honor of the European mathematician who discovered the numerical sequence that manifests itself (rather spectacularly) all throughout nature.
As far as dates go, 11/23 happens to be of particular significance to mathematicians and number nerds. It’s widely recognized as Fibonacci Day, because the numbers on the date match the first four numbers in the famed Fibonacci sequence.
In the Philippines, we tend to write dates the same way Americans do, so this can apply to us as well. (Think about it: It actually makes more sense for Filipinos to celebrate this than Thanksgiving Day.)
More than just giving math whizzes another odd holiday, though, Fibonacci Day serves an important purpose: to celebrate the inherent beauty of mathematics, and how we can observe it in day-to-day life. (If you’ve ever looked at a math lesson and wondered exactly how it would help you post-graduation, then keep reading, because this article’s for you.)
A hare-raising tale
The Fibonacci sequence is sophisticated in its simplicity. After the first two numbers (0 and 1), each succeeding number is the sum of the two numbers before it.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
This interesting sequence was first observed and described by Leonardo of Pisa, more commonly known as Leonardo Fibonacci. “Fibonacci” is short for “filius Bonacci” (“son of Bonaccio”). Fibonacci accomplished quite a few things, including making the Hindu-Arabic numeral system more popular with European audiences via his book Liber Abaci (“The Book of Calculations”).
However, he is most known for the discovery that bears his name — a story tied to, of all things, rabbits.
In the aforementioned book, the mathematician posed a seemingly simple problem.
Put two newborn rabbits (one male and one female) in an empty field, with the following conditions:
1. No rabbits die or are eaten by predators.
2. Each female reproduces every month, starting from the second month after her birth.
3. Every time a female reproduces, she gives birth to one pair of rabbits, a male and a female.
Given those parameters, how many rabbits will be in the field after one year?
To make it easier to understand the answer, check out this diagram:

Doing the math, we would end up with 233 pairs (or 466 rabbits) by the end of the 12th month. That’s a lot of lagomorphs!
The Fibonacci number in nature
Take any two successive numbers in the sequence, and their ratio will be almost exactly the same as the Golden Ratio (1.6). The Golden Ratio (also called the “divine proportion”) is regarded as a universal standard of beauty. To maximize aesthetic appeal, craftsmen base the length and width/breadth of their creations on the Golden Ratio. Consider the size and composition of many Greek temples (which tend to be 1.618 times as long as they are wide) or the Egyptian pyramids (as the base length of a pyramid is 1.618 times its height).
The Fibonacci sequence also manifests constantly in nature, almost without fail.
Check out the spiral shape of a nautilus shell.
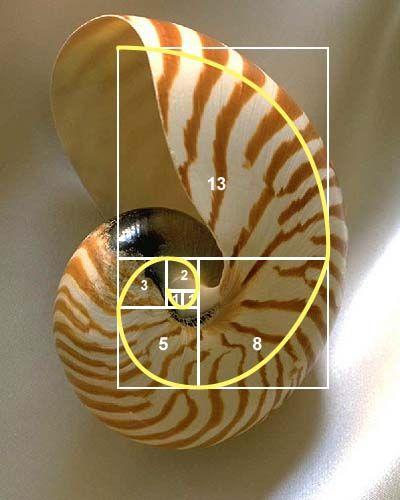
Here’s a tidal wave.

Take a look at these flowers, too.

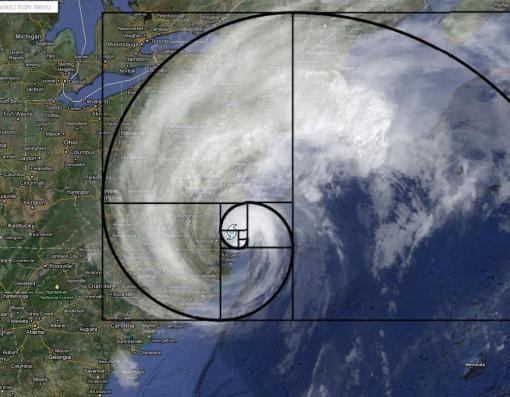
It’s in this hurricane as well.
Meanwhile, look at the way a tree’s branches grow.

Take the time to appreciate the beauty around you, because nature made it so. Trust the math guys on this one.
Cover photo: Three-shots/Pexels
References:
- http://sciencenotes.ucsc.edu/9402/Numbers.html
- http://www.mathscareers.org.uk/article/the-mathematics-of-rabbit-island/
- https://io9.gizmodo.com/5985588/15-uncanny-examples-of-the-golden-ratio-in-nature
- https://www.independent.ie/world-news/and-finally/happy-fibonacci-day-maths-fans-celebrate-number-sequence-mirrored-in-date-36347225.html
- https://www.theodysseyonline.com/7-beautiful-examples-fibonacci-sequence-nature
- https://www.timeanddate.com/holidays/fun/fibonacci-day
Author: Mikael Angelo Francisco
Bitten by the science writing bug, Mikael has years of writing and editorial experience under his belt. As the editor-in-chief of FlipScience, Mikael has sworn to help make science more fun and interesting for geeky readers and casual audiences alike.







